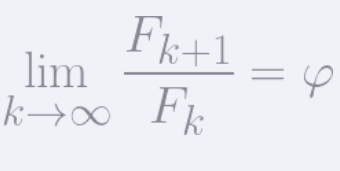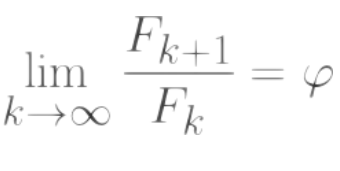When developing games, I often look for tools that allow fast prototyping, simple syntax, and strong community support. That’s why I chose the Lua programming language together with the LÖVE framework—a lightweight, open‑source 2D game engine. It’s particularly well‑suited for experimenting with game mechanics.
LÖVE Framework Basics
In LÖVE, the game loop is structured around three main functions:
- love.load() → runs once at the start, initializing the game.
- love.update(dt) → updates the game state every frame, where dt is the delta time.
- love.draw() → renders the updated state to the screen.
This simple structure makes it easy to integrate control algorithms directly into the update cycle.
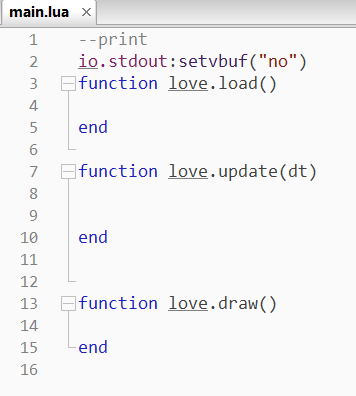
This minimal template is where I later integrated the PI controller logic. Notice the line at the top:

One of the classic game types I’ve always been fascinated by is the “bricks breaker” (or breakout/arkanoid‑style) game. Using this as a foundation, I built a prototype and then decided to take it a step further: I implemented a PI controller algorithm to automatically control the paddle.
Why PI Control in a Game?
In industrial automation, PID controllers are widely used to regulate systems with feedback loops. They combine three effects:
- Proportional (P): reacts to the current error.
- Integral (I): accounts for accumulated error over time.
- Derivative (D): predicts future error trends.
For this project, I focused on the PI controller (proportional + integral). My interest in PID control goes back to earlier experiments with Arduino boards and smart materials, where I used it for actuator position control. Bringing that concept into a game felt like a fun crossover between engineering and gameplay.
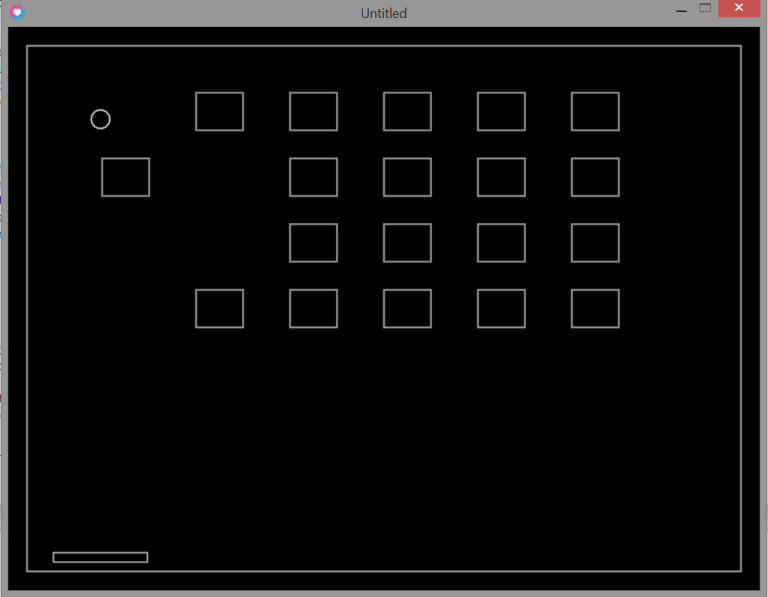
The Game Prototype
The layout includes:
- Rows of bricks at the top of the screen.
- A paddle at the bottom, which is normally player‑controlled.
- A ball that bounces around the playfield.
Implementing the PI Algorithm
The PI controller was applied to the paddle’s horizontal movement. The algorithm works by:
- Calculating the error between the ball’s x‑position and the paddle’s x‑position.
- Using Kp (proportional gain) and Ti (integral time constant) to compute the control signal.
- Integrating the error over time with a trapezoidal integration function (trapez_integral).
- Updating the paddle’s velocity based on the control output.
Instead of manually moving the paddle, the algorithm automatically adjusts its position to follow the ball. The result is a paddle that feels almost “intelligent,” smoothly tracking the ball’s trajectory.
Here’s the function I used to update the paddle’s position automatically. It runs inside the love.update(dt) loop:

How It Works
- Error calculation: The difference between the ball’s x‑position and the paddle’s center.
- Integration: Errors are accumulated over time using a trapezoidal method (trapez_integral).
- Control law: The paddle’s velocity is computed as a combination of proportional and integral terms.
- Update step: The paddle’s position is adjusted each frame, making it smoothly track the ball.
By tuning Kp and Ti, you can change how aggressively or smoothly the paddle follows the ball.
- A higher Kp makes it react faster but can overshoot.
- A smaller Ti increases the effect of accumulated error, improving accuracy but risking oscillation.
Even with just proportional control, the paddle follows the ball reasonably well. But adding the integral term makes the movement more precise and stable, reducing steady‑state error. Since the PI controller was sufficient, I didn’t include the derivative term.
The resulting equation for paddle velocity is essentially:
$$
Kp \cdot \left( e(t) + \frac{1}{Ti} \int_{0}^{t} e(t)\, dt \right)
$$
where:
- Kp = proportional gain
- Ti = integral time constant
- e(t) = error between ball and paddle positions
Numerical Integration with the Trapezoidal Rule
- To implement the integral part of the PI controller, I used a trapezoidal integration function. This method approximates the area under the error curve by summing trapezoids between successive time steps. It’s simple, efficient, and works well in real‑time applications like games.
- Here’s the Lua function:

How It Works
- Inputs:
- fonk → a table of error values over time.
- t → a table of corresponding time values.
- Loop: For each time step, it calculates the trapezoid area between two points.
- Output: Returns the accumulated integral of the error signal.
This integral is then used in the PI control law to adjust the paddle’s velocity, ensuring it doesn’t just react to the ball’s current position but also accounts for past errors.
The outcome: a paddle that automatically moves toward the ball with smooth, responsive behavior. It was both effective and fun to implement!

Final Thoughts
By combining game development with control theory, I ended up with a paddle that intelligently tracks the ball using a PI controller. It’s a small but exciting example of how engineering concepts can enrich gameplay mechanics. And honestly—it was just plain fun to see control theory come alive in a simple arcade game!
Resources I Used
- LÖVE Arkanoid Tutorial – step‑by‑step guide to building a breakout clone.
- Sheepolution’s LÖVE Tutorials – beginner‑friendly learning material.
- ZeroBrane Studio – the Lua IDE I used for development.
- Automatic Control: System Dynamics and Control Systems by Prof. Dr. İbrahim Yüksel – for deeper theoretical background.